Author: Robert Sloma, Sigma Advantage
Author: Robert Sloma, Sigma Advantage
Covestor model: Aggressive Stock
Over the last month or so, I have had several clients ask me why the portfolios I am managing for them are not beating the S&P 500 on a direct comparison basis, especially within a 1-year timeframe. Since the Fall, and definitely since the beginning of 2012, the investing environment has been very challenging. The market is not recognizing, or rewarding, any value.
Needless to say, it has been a frustrating experience for growth-oriented managers that have a value component to their investment process/strategy. This frustration is clearly expressed in a recent Morningstar interview with Eric Schoenstein, co-manager of the Jensen Quality Growth, who has seen a growing number of companies having the fundamentals worthy of his portfolio but says the market has given them little recognition.
Comparing return performance only looks at half of the picture regarding investments. Even though the financial services industry and the general media focus on return performance exclusively, doing so is very dangerous for the investor. The investor needs more to make an informed decision on whether an investment is performing better than a given benchmark, e.g. the S&P 500.
To obtain a full picture of an investment’s performance, the investment’s risk needs to be considered as well as its return performance. Over the next month, or so, I will present how an investor should measure a manager’s performance including the risk being taken as well as the return.
I will start with sharing part of a lecture I did this summer as part of a corporate finance course for Davenport University’s MBA program that shows the basic relationships between risk and return:
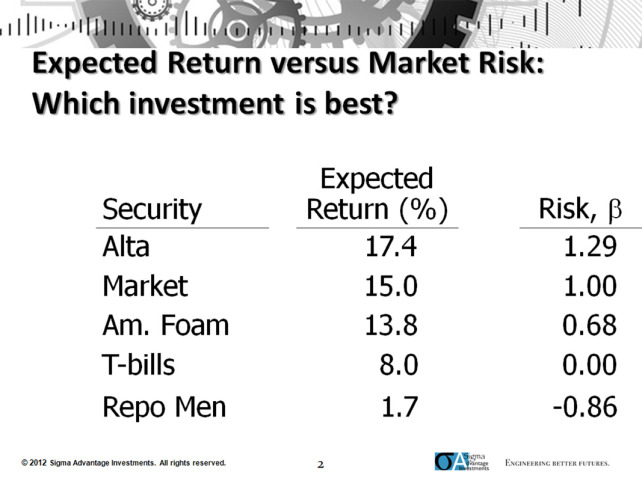
Take the example in Figure 1 above, where the expected returns for three companies are shown in relation to U.S. Treasury Bills and the general Market. The risk, as measured in this case by beta (β), for each item is also shown. So, the question is “Which is the best investment?.” This is a loaded question and is dependent on many factors. For the time being, we will assume the investor’s risk tolerance is not a factor in the decision. So the key is to come up with a rational, computation based process to determine the answer to this question.
Fortunately, we have Jack Treynor (1961, 1962), William Sharpe (1964), John Lintner (1965) and Jan Mossin(1966) to thank. All four independently introduce the capital asset pricing model (CAPM) that built on the work of Harry Markowitz related to the efficient frontier, portfolio diversification, and modern portfolio theory. The CAPM provides for a way to price a security or portfolio based on four factors, the risk-free rate (Rrf); the expected return of the market (benchmark, Rm); the expected return of the security/portfolio (Rs); and the security’s/portfolio’s beta (βs). In this case, we will utilize the security market line (SML) from CAPM. The SML is defined as follows:
Rs = Rrf + ( Rm – Rrf )βs;
where ( Rm – Rrf ) is also called the market risk premium.
So, if we assume Rrf = T-bills rate = 8% and Rm = 15% (both from Figure 1 above), then the market risk premium = 15% – 8% = 7%. We can use this and the security data from Figure 1 to calculate the required rates of return for each security. The required rate of return is the return that investors in the market require, based on the risk of each security captured in the security’s beta. The required rates of return are shown below in Figure 2.
Now we will compare the required rates of return against the expected returns for each security, shown in Figure 3:
Figure 3 shows that both the T-Bills and the Market are fairly valued, which we would expect since they made up the basic equation. (If you had not noticed, the SML equation defines a line, with the risk-free rate as the y-intercept and market risk premium as the slope.) Alta and American Foam are undervalued, since their expected returns are greater than the market required returns. Repo is overvalued since its expected return is less than the market required return.
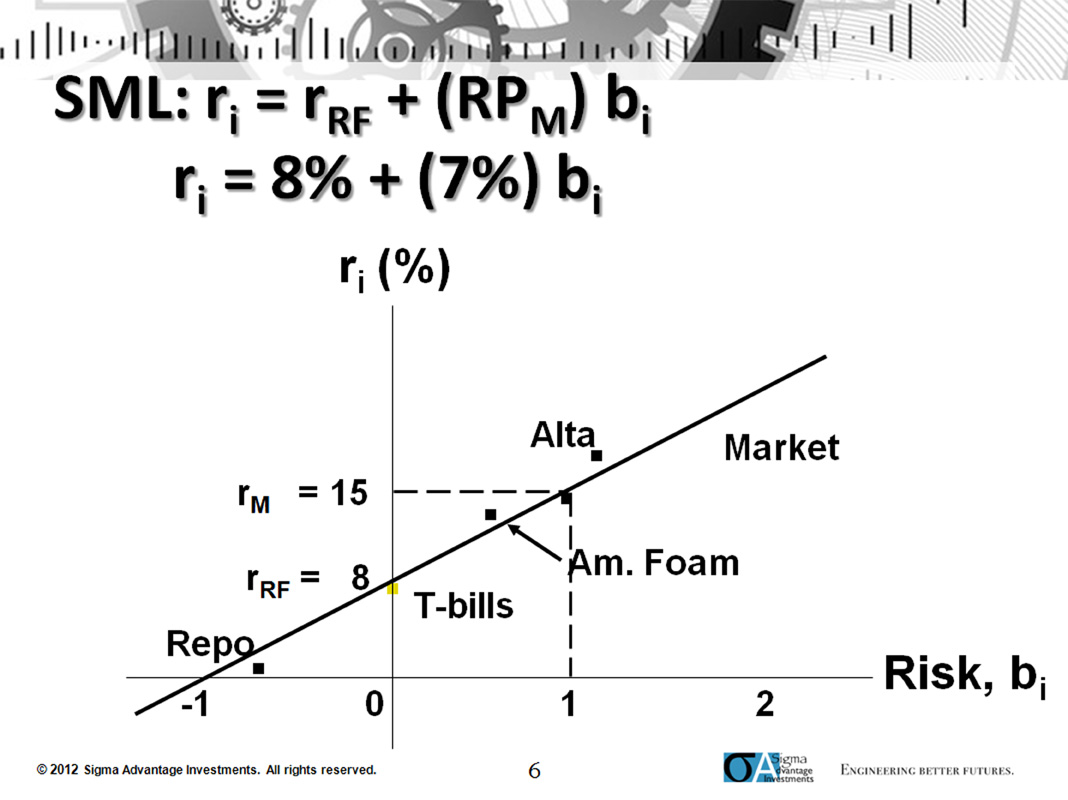
These relationships can be shown graphically, with each security plotted on a graph showing their expected return versus their beta, with the security market line going through the risk-free rate and the market (Figure 4).
Here we can see undervalued securities lie above the SML (Alta and American Foam), fairly valued lie on the SML, and overvalued securities lie below (Repo).
There are many detractors regarding the validity of the CAPM. Although many of the issues they present with CAPM are valid, my experience has been that it can be a useful tool. The concepts presented with the CAPM and efficient frontier as part of Modern Portfolio Theory can be utilized to make the asset allocation decision that will provide a significant chance of successfully outperforming the market (as measured by major benchmarks) over the long term. My next post will build on these concepts.